圖論、線性代數、團隊關係 從數學的角度切入並觀察團隊關係

前陣子小編參加讀書會，不小心看到了連通圖跟特徵向量，馬上想起了小時候周老上的數學，但卻回憶不了過去特徵值、特徵向量的物理意義，於是乎，這篇心得不就來了嗎!!!這篇文章會帶著大家一起從圖論、線性轉換、收斂系統的角度來看團隊關係。

收斂系統

在公司或職場中，工作技能的供給和需求兩個變數可以看成是一個線性且收斂的系統，前天晚上問了一下家小孩，宅條舉例通常三維以下的關係會是能夠收斂的，以草原上的獅子跟牛為例來說明。

首先假設一個 Control Volume 且在固定條件下的 Property 都是穩定的，也就是草原中草的溫度、濕度、草的生長速度都是穩定的，獅子跟牛是屬於吃與被吃的關係，最終獅子和牛會收斂在某種平衡。

如果因為獅子開聯誼派對導致下波出生的獅子較多，接下來牛被吃的量也會變多，當食物變少了獅子自然死亡的比例則會提高，每天的回合就像是個轉換矩陣，讓數量變化形成某種無限循環，然而獅子和牛的數量取決於:

• 獅子的掠食
• 獅子的自然死亡
• 牛的自然死亡
• 牛的出生速度

什麼是 Property? 在 Control Volume 中達到 Homogeneous 情況的 Steady State

來看看為什麼有些公司常常擴編了之後又裁員，當 Control Volume 中的 Property 都沒有進行改變時，像是高層的價值觀、公司的業務量等等都沒太大改變的情況下，工作技能的需求與供給就會像是獅子和牛一樣。以一個這樣的系統來說，特徵值就像是 Control Volume 的本質組成，會影響整個系統收斂的速度。

同理，為什麼團隊成員越多效率反而並不一定會提升，雖然總體獵捕的速度是加快的，但牛的數量有時候並沒有隨著一起變多，反而造成了團隊的總獵捕量的下降，這可能也是為什麼 Scrum Team 要維持在比較小的編制，除了溝通成本外，或許是為了讓收斂速度變快且更好預測吧?

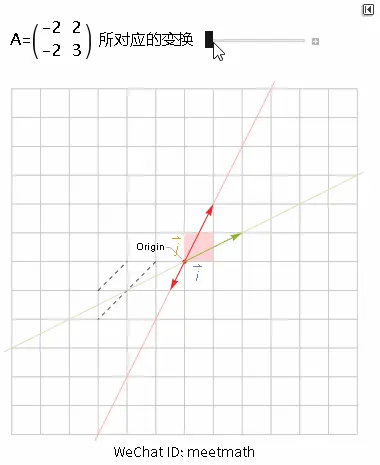
線性轉換

為什麼要進行轉換，通常就是在原來的觀察的時間或空間下並沒有那麼好觀察，像是把一般矩陣或是對稱矩陣做對角化，或是把三維降成二維，簡單來說棒球投出後的軌跡雖然是發生在三維世界，但實際上可以透過二維的平面進行描述，也就是大家國高中念的物理。

線性轉換，就是把線性的系統看成函數，探討在不同向量空間裡面向量的對應情形，轉換過後空間雖然扭曲改變了，向量與向量之間的關係並沒有改變，平行的還是平行，垂直的還是垂直。就像在自動控制系統中，我們也很常把時域轉換成頻域來進行觀察。

用數學的名詞來看就是在向量空間中透過轉換矩陣，進行向量、座標之間的轉換 AX = b，A 是轉換矩陣，幫我們把 X 轉換成 b，其中 X 是定義域，b 是經過線性轉換後的值域。

其實轉換和降維的想法我覺得蠻重要的，在遇到問題的時候，常常大家都說對人不對事 (更正是對事不對人)，反正遇到問題就先推卸責任說是其他 Team 的問題就對了，然而這種方式很可能會把自己養成廢物，但無腦的幫忙救火擦屁股也可能變成能者多勞 QQ

那公司的文化是否能提倡透過轉換和降維把人的因素去掉，去想一下這個問題怎麼避免和改善或許對團隊才是最重要的。當發生問題的時候，先不要想是人的問題，所以去掉這個維度之後，剩下的通常就是流程面、技術面的防呆，我個人是認為好的上 Code 流程以及一定程度的自動化導入完全可以大量降低出包風險。

討論需求的時候，PM 或是老闆的概念往往都是多維度的一個想像結果，身為不想加班且加班不能的工程師就必須協助把維度下降，降成一個最小可行性的解決方案，在最短的時間做持續的交付，讓專案用每天向終點爬一點的方式慢慢前進，而不是光討論和設計就花了兩週以上然後叫工程師要在三周內衝完全部，這種比例跟專案進行方式明顯會增加工程師的疲累感和出包機率。

特徵值與特徵向量

特徵向量是經過線性轉換 (旋轉、拉伸) 而不改變方向的一個向量，滿足條件的向量可以用 A(x) = λx 來表示。

特徵值與特徵向量 (圖片來源)

那 λ 就會出現以下三種情境，理工科的大大們一定不只有點熟悉，在阻尼系統中就代表欠阻尼(Underdamping)、臨界阻尼(Critically damped)、過阻尼(Overdamping)，但只是跟係數相關，正確算法可能要參考這裡XDDD

• λ < 1
• λ = 1
• λ > 1

阻尼係數 (圖片來源)

小時候我們學過的撿鞋運動 f(x) = -kx 就是類似這樣的公式，從物理學可以知道加速度跟時間的關係是軌跡方程式微分兩次，如果用成人の數學去解出 x(t) 就會發現是 cos 和 sin 的組合函數。

Wiki: https://zh.wikipedia.org/zh-tw/%E5%B8%B8%E5%BE%AE%E5%88%86%E6%96%B9%E7%A8%8B

實際上舉個經典例子來看，被震斷的橋梁就是系統中的幾個部分被鎖死的阻尼系統。

會造成震動的原因是風力在原來穩定的流體中，被放了一個障礙物，在滿足某些條件下 (印象中是不滑動條件)，流體會出現邊界層的流動分離，接著分離的流體就會出現高低壓差，產生渦旋，在障礙物的兩側會產生規律的反向渦旋，就是 Kármán vortex，就是這個穩定頻率的壓差變化讓橋倒塌 (影片 50 秒左右)。

Wiki: https://zh.wikipedia.org/zh-tw/%E5%8D%A1%E9%97%A8%E6%B6%A1%E8%A1%97

如果大家好奇，台南美術館二館觀景台上的欄杆都只有做單一維度的支撐，大家下次有到台南玩可以用小小力量還有特定頻率去輕輕的推，推久了就會發現晃動越來越大，然後就不要再推了因為會壞掉 XDDD

就跟盪鞦韆的道理一樣，找出適合那個人體重晃動的基頻，而特徵值在這裡其實就會跟自然振動頻率相關，其中最小的那個就是基頻，在音樂裡面泛音頻率就正好是基頻的整數倍，通常在譜曲時會用頻率上的整數比來讓整體音樂和諧，可以參考基頻與泛音。

在團隊關係中，要怎麼讓開會時不要一直發散也不要太快結束呢? 我到最近幾年漸漸都在推廣大家在開會前先寫好會議記錄，在還沒開始開會前就直接寫上想像中的結果上去，沒有結果就提出問題的分析以及需要的協助，調整撰寫會議紀錄時間就是一個調整參數的概念 XD

圖論

在 50 人以下的新創公司裡，我的經驗是每個人做的事情都非常透明，只要你想看的話幾乎都知道每個人現在在做什麼，即便想藏也藏不起來，但場景只要一變成 50 人的中小企業，要了解其他部門往往就變成需要主管來進行同步，等到變成 300 人上櫃公司之後，我發現，竟然變成需要靠內部八卦跟小道消息了…

這時候就會讓人好奇，為什麼公司會越來越走向資訊不對稱這條路?

其實顯然就是有人在溝通網路裡面在操作這樣的事情，在圖論中有種圖的定義是連通圖，定義是對於所有點對之間都至少有一條路徑可以相通。在組織中可以看成訊息的溝通網路，如果加上限制就會變成有向圖，舉例來說就像是商朝末年，紂王耳朵只會透過妲己的嘴巴吸收訊息，最終結果是微子去之，箕子為之奴，比干諫而死。

在圖論和網絡分析中，中心性 (Centrality) 是判斷網絡中節點重要性或影響力的指標，無能力者絕對要努力在組織中成為連通圖的中心，雖然容易讓訊息的流通遇到瓶頸，但如果想要搞政治穩固自己的位置絕對是不二選擇。

在建立團隊的時候，為了降低溝通成本，就可以用最小生成樹的概念，讓訊息可以無痛的在節點中建立連接，最小生成樹是連通加權無向圖中一棵權值最小的生成樹，並告訴團隊成員，怎麼用最短的路徑通知到該通知的節點，不管是透過 Trello、Jira、Slack 的 Stand up Alice 我覺得都是不錯的工具。

另外如果一個有向圖中的每一個頂點對於其他的每個節點都存在著一條路徑能夠到達，可以稱該有向圖強連通，而強連通元件的性質是可以把整個強連通元件視作一個點，如果將每一個強連通元件縮成一個點，則原圖會變成一張有向無環圖。

強連通的這個部分，個人覺得這個資訊高速流通有點像是網路業中的 Scrum Team。

中心性

• Degree Centrality: 重要的節點就是擁有許多連接的節點，連接關係越多，影響力就越強，助理是大家的，非常重要
• Closeness Centrality: 接近中心性，該節點與圖中所有其他節點之間的最短路徑長度之和的倒數，東廠第一把交椅
• Betweenness Centrality: 中介中心性，圖中任兩節點均至少存在一個最短路徑，中介中心性即為這些最短路徑穿過該節點的次數，好人一生平安，上廁所都有衛生紙，有點像是超強 PM 或是 Scrum Master
• Eigenvector Centrality: 特徵向量中心性，是測量節點對網絡影響的一種方式，得分較高意味著該節點與許多自身得分較高的節點相連接，婆婆媽媽們の八卦領袖

網路流

在 Network Flow and Maximum Flow Minimum Cut Theorem 裡面，還加上了流量的概念，中心這時候就不一定重要，因為會存在資訊流量限制，可以想像成助理雖然是大家的樞紐中心，但權責上僅能處理小問題。

假設水管系統水從入口流入，經過互相連結、孔徑不一的水管後從出水口流出。但目標是一次流入最大量的水。若先流過一條半徑只有 2 公分的水管，則接在其後的水管的半徑即使再大，水流量仍會被半徑 2 公分的水管所限制，因此整體流量也就受限制。

個人認為團隊中要找到資訊流的瓶頸，通常就是先看一下樞紐中心是不是在搞資訊不對稱，如果發現是東廠第一把交椅，可能也只能想辦法另外打通一條資訊的連通網路 QQ

• ← 上一篇
• 下一篇 →